Was ist der Break-even-Point? Und wie wird er grafisch ermittelt? Finden Sie in unserem Wiki-Beitrag die Formel und Beispiele zur einfachen Berechnung des BEP.
Was ist der Break-even-Point?
Der Break-even-Point (BEP) bezeichnet den Punkt, an dem Erlös und Kosten gleich hoch sind. An dieser Stelle wird kein Gewinn, aber auch kein Verlust erwirtschaftet, da die Kosten und die Erlöse genau gleich sind. Aus diesem Grund stellt dieser Punkt die Gewinnschwelle oder auch die Gewinngrenze dar. Er besteht aus den Nullstellen der Gewinnfunktion. Die obere Nullstelle ist die Gewinngrenze und die untere die Gewinnschwelle. Bei einer Überschreitung der Gewinnschwelle gibt es einen Gewinn und bei der Erreichung der Gewinngrenze einen Verlust.
Um die Effizienz eines Produktes herauszufinden, führt ein Unternehmen eine Gewinnschwellen-Analyse durch. Dabei wird berechnet, wie viele Produkte produziert und verkauft werden müssen, um alle Kosten zu decken. So ermitteln Sie die Absatzmenge. Um einen Gewinn zu erwirtschaften, wird außerdem der benötigte Umsatz analysiert.
Mit der Break-even-Formel berechnen Sie den Absatz, der für die Gewinnschwelle benötigt wird:
Absatzmenge (X) = Fixkosten/ (Verkaufspreis – variable Stückkosten)
Wenn die Gewinngrenze erreicht ist, ist gleichzeitig der Deckungsbeitrag so hoch wie die Fixkosten. Die Einnahmen aus dem Verkauf reichen aus, um die Kosten für alle zu decken.
Grafische Ermittlung des Break-even-Points
Um den Break-even-Point grafisch zu ermitteln, zeichnen Sie Fixkosten, variable Kosten und die Verkaufserlöse in ein Diagramm ein.
Beispiel:
Die Mustermann AG hat ein Startup gegründet und möchte wissen, ab welcher Stückzahl verkaufter Süßigkeiten sie Gewinn erzielt. Folgende Produktionskosten fallen an:
Fixkosten: 5000€
Die Fixkosten beschreiben die Kosten, die in jedem Fall anfallen, unabhängig von der tatsächlichen Produktion.
Variable Kosten: 0,90€
Die variablen Kosten sind die Kosten, die anhand des Beschäftigungsgrades oder der Produktionsmenge entweder fallen oder steigen.
Verkaufserlös: 2€
Der Erlös beschreibt die Einnahmen pro verkauftem Produkt.
Haben Sie die einzelnen Werte ermittelt, trage Sie diese am besten in eine Tabellenkalkulation ein, um sich das Zeichnen des Diagrammes zu erleichtern. In unserem Beispiel sähe das so aus:

Lassen sie Excel oder ein ähnliches Kalkulationsprogramm aus dieser Tabelle ein Liniendiagramm erstellen.
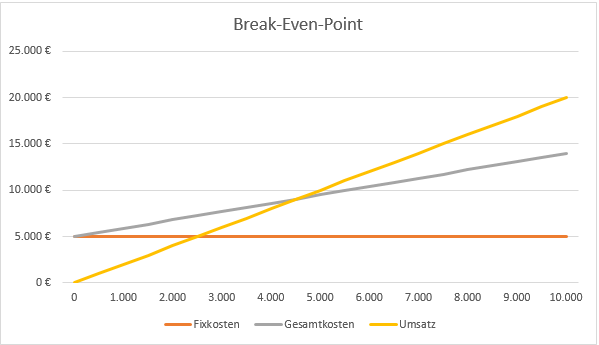
Wo sich Umsatz und Kosten treffen, befindet sich der Break-even-Point! Wie man erkennen kann, überschneiden sich Umsatz und Kosten ungefähr bei 4.500 Stück. Den exakten Wert erhalten Sie über die rechnerische Variante.
Formel zur Berechnung des Break-even-Points
Zur Berechnung der Gewinnschwelle ist eine Unterscheidung der Kosten in variable und fixe Kosten notwendig, die in einer speziellen Formel eingefügt werden. Außerdem muss der Deckungsbetrag bekannt sein. Er wird verwendet, um zu bewerten, wie viel ein einzelnes Produkt oder eine Dienstleistung zur Deckung der festen Kosten eines Unternehmens beiträgt, nachdem alle variablen Kosten abgezogen wurden.
Durch eine Break-even-Analyse ist die Auswirkung der Gewinnziele auf Preis und Kapazitäten ermittelbar. Dadurch lassen sich Zusammenhänge besser erkennen. Folgende Formel wird dafür verwendet:

Der Break-even-Point befindet sich also genau dort, wo aus der finanziell negativen Entwicklung eine steigende und somit positive Kurve wird. Betrachtet man den Break-even-Point aus mathematischer Sicht, beschreibt dieser die Nullstelle der Gewinnfunktion eines Unternehmens. In der Praxis findet der Break-even-Point seine Anwendung beispielsweise in der Investitionstätigkeit von Unternehmen. Sobald die erzielten Einnahmen alle Kosten decken, wird die Investition ab diesem Punkt rentabel. Daher spielt die Berechnung des BEP besonders im Bereich des Controllings eine wichtige Rolle..
Beispiel zur Berechnung des Break-even-Points
Die Mustermann AG hat ein Startup gegründet und möchte wissen, ab welcher Stückzahl verkaufter Süßigkeiten sie Gewinn erzielt. Für die Produktion fallen 5.000 € Fixkosten und 0,90 € variable Kosten an. Der Verkaufserlös pro Produkt liegt bei 2 €. Der Deckungsbeitrag errechnet sich durch die Subtraktion des Verkaufspreises pro Stück und den variablen Kosten. Somit ergibt sich ein Deckungsbeitrag von 1,10 Euro. Für die Gewinnschwelle teilt man die Fixkosten durch den Deckungsbeitrag und erhält einen Break-even-Point bei 4.545,45 Stück.
Ist eine Break-even-Analyse auf Tagesbasis sinnvoll?
Eine Break-even-Analyse auf Tagesbasis kann in bestimmten Situationen nützlich sein. Jedoch gibt es einige Einschränkungen, die berücksichtigt werden sollten:
- kurzfristige Schwankungen verstehen: Tägliche Analysen können hilfreich sein, um kurzfristige Schwankungen in der Nachfrage oder im Umsatz zu verstehen. Dies ist besonders relevant in Geschäften mit stark variierender täglicher Nachfrage, wie z. B. bei einem Eisverkäufer, bei dem das Wetter einen großen Einfluss hat.
- operationelle Anpassungen: Eine tägliche Analyse kann nützlich sein, um operationelle Entscheidungen zu treffen, wie z. B. die Personalplanung oder die Lagerhaltung.
- Einschränkungen:
- langfristige Trends werden vernachlässigt: Eine Fokussierung auf den täglichen Break-even kann langfristige Trends und strategische Ziele übersehen.
- Variabilität ist nicht repräsentativ: Tägliche Ergebnisse können stark variieren und sind möglicherweise nicht repräsentativ für den langfristigen Geschäftserfolg.
- aufwändige Verwaltung: Die tägliche Durchführung einer Break-even-Analyse kann zeitaufwendig und möglicherweise nicht effizient sein, besonders für kleinere Unternehmen.
- alternative Zeitrahmen: Oft ist es sinnvoller, den Break-even-Point über einen längeren Zeitraum wie monatlich oder jährlich zu analysieren. Dies ermöglicht eine ganzheitlichere Sicht auf die Geschäftsleistung und minimiert die Auswirkungen von kurzfristigen Schwankungen.
Zusammenfassend kann eine Break-even-Analyse auf Tagesbasis in bestimmten Geschäftsbereichen mit hoher täglicher Variabilität nützlich sein. Allerdings sollte sie ergänzend zu längeren Analyse-Zeiträumen wie innerhalb eines Monats oder eines Jahres verwendet werden, um ein umfassenderes Verständnis der Geschäftsleistung zu gewährleisten.
Fazit: Break-even-Point
Der Break-even-Point bietet eine schnelle Übersicht darüber, ab wann Investitionen für Unternehmen rentabel werden. Daher sollte auch vor jeder Investition in Betracht gezogen werden, den Break-even-Point zu berechnen.
